The predictive power of equilibrium exchange rate models
Published as part of the ECB Economic Bulletin, Issue 7/2021.
1 Introduction
Central banks carefully monitor the evolution of exchange rates. In the case of the European Central Bank (ECB) and other major central banks, the exchange rate is not a policy target. But the “market value” of the euro is highly relevant for understanding the medium-term inflation outlook via its impact – through import prices and through general equilibrium effects – on the real economy.
It would therefore be very useful to be able to anticipate future exchange rate movements, but this has proven rather elusive, especially at short horizons. The view that exchange rates are largely disconnected from economic fundamentals at short horizons has mainly predominated since the seminal paper by Meese and Rogoff (1983), which showed that exchange rate models were unable to deliver more accurate nominal exchange rate forecasts than the simple prediction of “no change” associated with the random walk (RW) model.[2] The difficulty of predicting exchange rates with systematically better results than by using the RW model, especially at short-horizons, was reiterated by Rogoff (2008)[3] and, more recently, in the influential articles by Rossi (2013)[4] and Cheung et al. (2019)[5].
Exchange rates have an important role beyond their key contribution to understanding the inflation outlook. While, in line with their monetary policy strategies, the ECB, the US Federal Reserve System and other major central banks do not treat the exchange rate as a target variable,[6] they are mindful that if large and persistent nominal exchange rate fluctuations occur, real exchange rate misalignments may develop over time that could have significant implications for the economic outlook. This is because over- and undervalued currencies, in an environment of price rigidity, could lead to competitiveness imbalances, excessive real exchange rate volatility and, potentially, sharp economic adjustments with adverse effects on consumption and production.[7] This is the context in which currencies’ “fair value” is often discussed. In exceptional instances, major central banks have intervened directly or only verbally in foreign exchange markets in a concerted manner to influence exchange rate dynamics. It is hence not surprising that academics and policymakers have continued to strive in recent decades to improve their methodological frameworks for assessing equilibrium exchange rates (e.g. Bussière et al., 2010; Phillips et al., 2013; Fidora et al., 2017; Couharde et al., 2018; and Cubeddu et al., 2019).[8]
Recent papers have argued that concepts of equilibrium exchange rates, besides their intrinsic interest, could be helpful for understanding and predicting exchange rate movements. These papers suggest that, even if the dynamic adjustment of exchange rates cannot be fully anticipated, it is known that they should eventually adjust to their equilibrium, i.e. a terminal condition defined by economic theory. For example, Ca’ Zorzi et al. (2016) and Ca’ Zorzi and Rubaszek (2020)[9] show that it is sufficient to assume that the real exchange rate gradually converges to the simplest definition of the equilibrium exchange rate, i.e. relative purchasing power parity (PPP), to produce surprisingly accurate real and nominal exchange rate forecasts. In theory, this approach is best suited to predicting real exchange rates, as the concept of the equilibrium exchange rate is defined in real terms. But empirical evidence shows that real exchange rate adjustments occur primarily through currency movements rather than via relative price changes. Thus, at least for countries with moderate inflation rates, measures of real equilibrium exchange rates can also be employed to forecast nominal exchange rates.[10] From a different starting point, Ca’ Zorzi et al. (2017)[11] and Eichenbaum et al. (2020)[12] suggest that more advanced macroeconomic models, known as dynamic stochastic general equilibrium (DSGE) models – which assume that real and nominal exchange rate fluctuations are driven by differences in the monetary policy stance adjusted for risk premia – also offer a fairly good description of exchange rate dynamics and perform well overall in forecasting real and, to a lesser extent, nominal exchange rates. The explanation for this is that, like simpler approaches, such models imply a gradual return of the real exchange rate toward its equilibrium PPP value, but they tend to underestimate the empirical regularity of a strong co-movement between real and nominal exchange rates.
The key question addressed in this article is whether concepts of equilibrium exchange rates other than PPP might strengthen the predictability of exchange rates. To the extent that long-term drivers of exchange rates can be understood, and hence the equilibrium exchange rate can be estimated more precisely, it should in theory be possible to better forecast the future trajectory of the real and nominal exchange rate. For that purpose, this article evaluates the predictive power of three popular equilibrium exchange rate models. Besides the PPP model, we also investigate simplified versions of the behavioural equilibrium exchange rate (BEER) and the macroeconomic balance (MB) approaches along the lines of Ca’ Zorzi et al. (2022).[13]
2 Three methods for assessing equilibrium exchange rates
Equilibrium exchange rate models are employed to decompose the real exchange rate ( ) into its equilibrium ( ) and misalignment ( ) components:

The split between the two components depends in part on the time horizon that is used. As discussed by Driver and Westaway (2005), exchange rate movements are driven by long, medium and short-term economic fundamentals and by an unexplained component.[14] The approach taken in this article is to distinguish between movements of the equilibrium exchange rates, and movements of the exchange rate around the equilibrium. The former are driven by long and medium-term economic fundamentals, while the latter are driven by short-term fundamentals and an unexplained component. This is consistent with theoretical general equilibrium models,[15] in which over the business cycle fluctuations in exchange rates around their equilibria are partly driven by central banks’ relative monetary policy stance, adjusted for risk premia.[16] The definition of equilibrium exchange rates is hence important from a monetary policy perspective.
The first equilibrium exchange rate model considered here is the PPP model, i.e. the oldest theory of real exchange rate determination, which was restored to prominence in modern times by Gustav Cassel and is still today a key benchmark for determining exchange rate parities in fixed exchange rate regimes.[17] In a nutshell, the PPP model starts from the law of one price, which states that international arbitrage helps to equalise the price of any tradable product denominated in a common currency. The concept of strong PPP emerges from applying this law to consumption baskets, i.e. the same basket of goods should cost the same across countries when denominated in a common currency. In contrast, the weak version of PPP theory states that, in equilibrium, the relative cost of the same basket of goods across countries is constant over time but might deviate from unity owing to factors such as taxes and/or transportation costs. The weak version of PPP is empirically more relevant and appealing from a practical perspective, as it implies that a long-run sample mean of the real exchange rate is a good proxy for the PPP-based equilibrium real exchange rate.
The BEER model generalises PPP theory by assuming that persistent PPP deviations should not be treated as “disequilibria” if they are driven by economic fundamentals. In other words, while the PPP model suggests that the long-term equilibrium exchange rate is a constant, in the BEER model the medium-term equilibrium fluctuates over time in line with changes in a set of economic fundamentals. In practice, the level of the BEER is estimated from a regression linking the real exchange rate to a set of economic variables indicated by economic theory considerations (Fell, 1996; MacDonald, 1998; Maeso-Fernandez et al., 2001; and Lee et al., 2008).[18] The literature has discussed at length the best choice of fundamentals for the BEER and the expected sign and magnitude of the parameters (for a comprehensive literature review, see Fidora et al., 2017).[19] In this analysis the choice of economic fundamentals is limited to three key ones: relative per capita GDP, net foreign assets and the terms of trade. All three variables aim to explain medium and long-term exchange rate movements while, as discussed above, the analysis does not include real interest rate differentials, fiscal variables or other short-term factors. In most of the literature it is taken for granted that a rise in relative per capita GDP ( ) leads to an appreciation of the real exchange rate. The explanation is twofold. From a demand perspective, an increase in relative income should lead to stronger demand for domestic non-traded goods and hence to an increase in their price relative to traded goods, i.e. a real exchange rate appreciation. The supply perspective is based on the Balassa-Samuelson effect, which suggests that a relative increase in productivity in the production of tradable goods leads to an increase in and a real exchange rate appreciation (Lee et al., 2013; and Zhang, 2017).[20] Another frequently cited explanation for long-run trends in equilibrium real exchange rates emphasises the role of net foreign assets ( ). The rationale is that a rise in increases the interest income on the current account that must be counterbalanced by a trade balance deterioration, requiring in turn a real exchange rate appreciation (Lane and Milesi-Ferretti, 2002).[21] The terms of trade ( ) is the third most used explanatory variable in BEER regressions. A rise in should lead to an improved trade balance, and therefore a real exchange rate appreciation is needed to restore the trade balance to its initial level. For the above reasons we estimate the level of the BEER with the specification used by Faruqee (1995) and Lane and Milesi-Ferretti (2004),[22] so that the value of the BEER for country i in period t is given by:

where all explanatory variables are expressed relative to a trade-weighted average of foreign values and the estimated signs of the regression match the theoretical predictions.
The MB approach defines equilibrium exchange rates from a current account sustainability perspective. The methodology of the MB approach differs substantially from that of the PPP and BEER models. Instead of estimating an equilibrium exchange rate, the MB approach estimates or calibrates/postulates an equilibrium current account (or norm) and the current account gap, i.e. the distance of the current account from this norm.[23] It then seeks to estimate or calibrate a relationship between the current account balance and the real exchange rate in order to establish to what degree the real exchange rate needs to adjust so as to close the current account gap. For that reason, this definition is closely connected with the debate on global (current account) imbalances and the role played by the exchange rate in unwinding them. Technically, to calculate the equilibrium exchange rate with the MB framework, three issues must be addressed. The first consists of projecting the level at which the current account balance would stabilise if exchange rates remained unchanged and output gaps were closed ( ). The second relates to setting the current account norm ( ), which is typically estimated using a panel data regression with similar fundamentals to those chosen for the above-mentioned BEER regressions. The third is estimating how changes in the real exchange rate affect the current account (elasticity ). Addressing these issues as in Ca’ Zorzi et al. (2022),[24] the equilibrium exchange rate ( ) can then be simply computed as:

Equation (2) reveals the critical role played by the current account elasticity , which measures the current account adjustment in response to a 1% exchange rate appreciation. For example, doubling the value of this elasticity would halve the exchange rate adjustment required to bring back the long-run value of the current account ( ) to its norm ( ). The academic literature has shown that the value of the current account elasticity is uncertain and dependent on some critical assumptions about the extent to which exchange rate changes pass through to export and import prices.[25]
In terms of country coverage, the analysis in this article includes the group of advanced economies that issue so-called G10 currencies, namely Australia (AU), Canada (CA), Switzerland (CH), the euro area (EA),the United Kingdom (UK), Japan (JP), Norway (NO), New Zealand (NZ), Sweden (SE) and the United States (US) and our quarterly dataset spans the period between the first quarter of 1975 and the fourth quarter of 2020. Such a sample is comparable to those used in studies evaluating exchange rate trading strategies for the ten globally most traded currencies (e.g. Opie and Riddiough, 2020), as well as recent studies on exchange rate forecasting (e.g. Engel and Wu, 2021).[26] There are two additional criteria for the country selection, namely the presence of flexible exchange rate regimes for most of the sample and the availability of sufficient macroeconomic data for a meaningful forecast evaluation exercise.[27] A full description of the data sources, estimated regressions and equilibrium exchange rate estimates is available in Ca’ Zorzi et al. (2022), which for the purpose of this article was updated to the fourth quarter of 2020.
3 In-sample adjustment
A key question considered in our analysis is to what extent the euro, the US dollar and other major currencies tend to converge to their long-run exchange rate equilibria. For each equilibrium exchange rate model, currency and horizon we estimate the parameters of the local projection regression:

in which the parameter measures the average fraction of misalignment eliminated at horizon . If the real exchange rate reverts to its equilibrium over time, the value of should converge to 1 as increases. In parallel, we estimate the local projection:
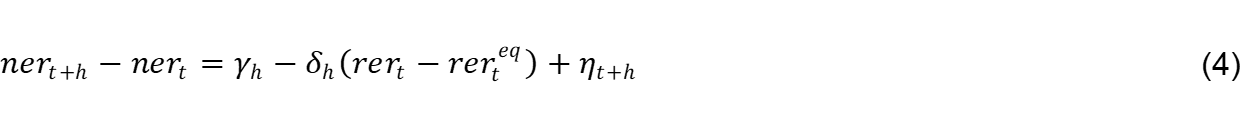
which enables the extent to which the nominal exchange rate accomplishes the required adjustment to be evaluated.
The evidence points to a clear tendency for exchange rates to converge to their equilibrium and for the pace of the convergence to be model-dependent. In Table 1, for each country the first line reports the fraction of the real exchange rate misalignment absorbed by the real exchange rate change ( and the second line reports the fraction absorbed by the nominal exchange rate change ( at each horizon .
Table 1
Fraction of the adjustment achieved by the real and nominal exchange rates relative to the initial misalignment across models

Source: Authors’ calculations.
Notes: The table presents the estimates of adjustment parameters
and
from regressions (3) and (4). Asterisks ∗∗∗ , ∗∗ and ∗ denote respectively the 1%, 5% and 10% significance levels. The panel comprises all of the G10 currencies.
Four interesting findings are evident from Table 1:
First, the adjustment of the real exchange rate starts almost immediately. In the case of the PPP model, for example, in one quarter the real exchange rate moves to absorb 7% of the real exchange rate misalignment for the euro and 5% for both the US dollar and the full panel of G10 currencies.[28] The adjustment is similar and marginally stronger in the case of the BEER model. It is remarkable that within the short horizon of one quarter a small fraction of the required exchange rate adjustment is already accomplished. It is hence not the case – despite being often stated – that short-run exchange rate movements are entirely unpredictable. The adjustment toward equilibrium is very slow but starts well before the one-year horizon.
Second, nominal exchange rate changes are at least in part predictable. The reason for this is that the required real exchange rate adjustment takes place via currency movements and not via an adjustment in relative prices across countries. This is apparent from the observation that the fraction of adjustment completed by the nominal exchange rate is almost as sizeable as the fraction achieved by .[29] In the case of the PPP model, the numbers are only slightly lower than for the real exchange rate: the nominal exchange rate absorbs 5% of the real exchange rate misalignment in the case of the euro and 4% for both the US dollar and on average for the panel. This is true across different models and horizons irrespective of the degree of exchange rate predictability, which differs across models.
Third, the pace of the adjustment toward the equilibrium varies considerably across models. With the PPP model, within three years the real exchange rate absorbs 72% of the required adjustment for the euro, 74% for the US dollar and 56% for the full panel of G10 currencies. However, the pace of adjustment is not the same for different equilibrium exchange rate concepts. It is somewhat stronger for the BEER model: within three years 79% of the adjustment is completed for the euro, 90% for the US dollar and 69% for the full panel.[30]
Fourth, the pace of the real exchange rate adjustment is much weaker with the MB model. After three years it is basically nil for the euro, 48% for the US dollar and only 24% for the full panel. This suggests that the in-sample explanatory power of equilibrium exchange rates estimated with the current account-based model is overall very poor. A similar pattern emerges if we focus on the adjustment of the nominal exchange rate (see Table 1).
Finally, there is an elegant graphical equivalent way to show that nominal exchange rates over time absorb past exchange rate misalignments. Below we produce a set of scatter plots showing nominal exchange rate changes at different horizons against the initial real exchange rate misalignment, i.e. the deviation of the real exchange rate from its model-consistent equilibrium value. To the extent that there is an adjustment, this relationship should be negative, and, in the case of full adjustment accomplished by the nominal exchange rate and no movements in the equilibrium exchange rate, the slope of the regression should be equal to minus one. Chart 1 shows the results for the three models at different time horizons, indicating with yellow circles the observations for the US dollar, with blue circles those for the euro and with red circles those for all other G10 currencies.
Chart 1
Scatter plot of nominal exchange rate changes vs. misalignments for the euro, the US dollar and all other G10 currencies
(percentage changes)

Source: Authors’ calculations.
Notes: The x-axis of the chart represents deviations of real effective exchange rates from their full-sample equilibrium, whereas the y-axis represents subsequent real exchange rate adjustments. The US dollar and the euro are marked with yellow and blue circles respectively. All other G10 currencies are marked with red circles. The diagonal line represents perfect adjustment to the equilibrium.
The chart confirms visually that for both the PPP and BEER models there is an adjustment mechanism at play, which ensures that the initial real exchange rate misalignment is absorbed through a nominal exchange rate movement. This is already visible at the one-year horizon and becomes particularly evident at longer horizons. For the MB model the adjustment is again much weaker and visible only for the US dollar at the five-year horizon.
4 Out-of-sample evidence
The evidence that exchange rates converge to their long-term equilibria begs the key question: can this information be exploited to forecast real and nominal exchange rates? To find the answer, in the next step we evaluate the out-of-sample forecast accuracy for horizons ranging from one to 20 quarters ahead in the period from the first quarter of 1995 to the fourth quarter of 2020 on the basis of our full panel of data. In particular, for each vintage period s, the local projection regressions (5) and (6) are employed to calculate forecasts for real and nominal exchange rates:

where , , , , and are the parameters and equilibrium exchange rate estimates based on a sample ending in period .
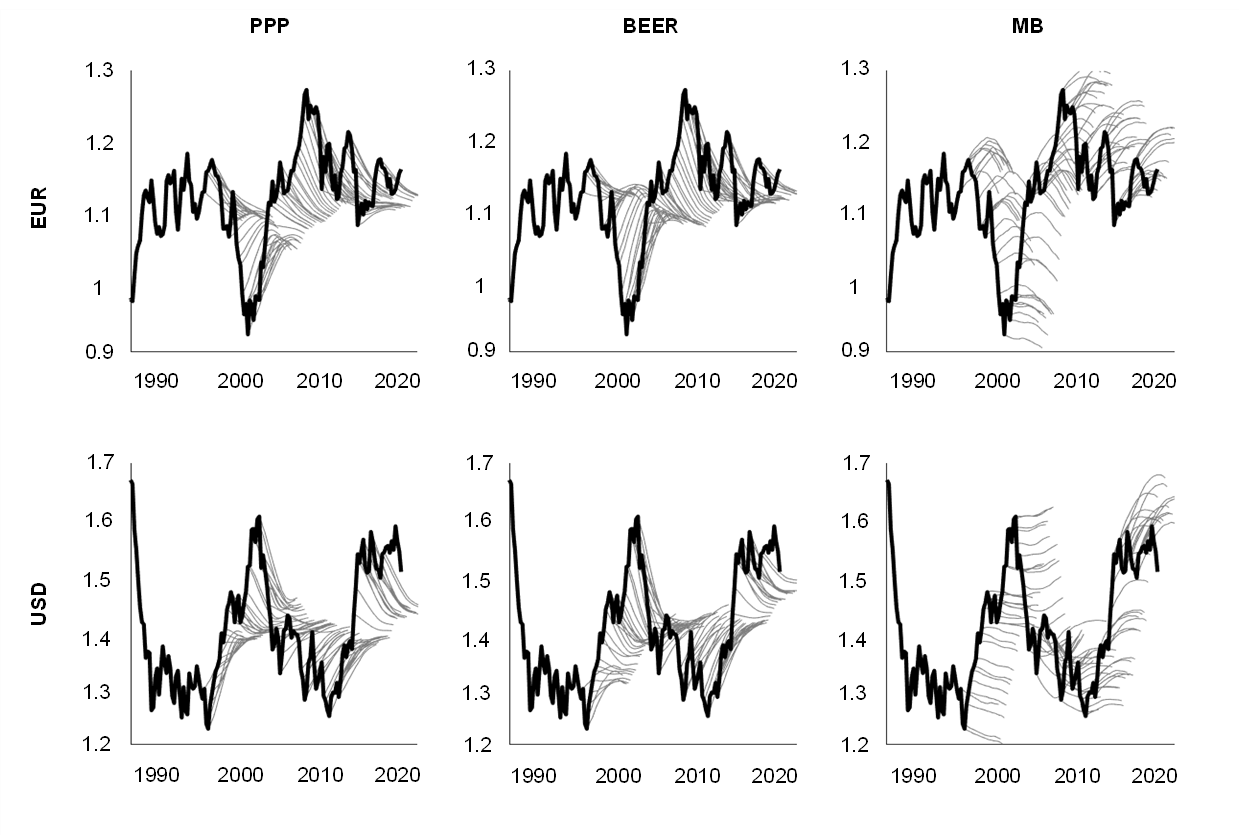
The chart showing sequential forecasts illustrates the predictive content of three equilibrium exchange rate models and immediately indicates that the PPP and BEER models perform relatively well. Chart 2 presents sequential forecasts for the US dollar and the euro. It shows that by predicting a gradual reversion of the real exchange rate to the corresponding equilibrium, the PPP and BEER models both usually deliver relatively accurate forecasts. By contrast, the MB model performs poorly[31] as forecasts obtained from this model are only weakly correlated with subsequent outcomes.[32]
Chart 2
Sequential forecasts
(log of the real effective exchange rate)
Source: Authors’ calculations.
Note: The black line represents the actual outcome while the grey lines represent the 20-quarters ahead forecast calculated at different points in time.
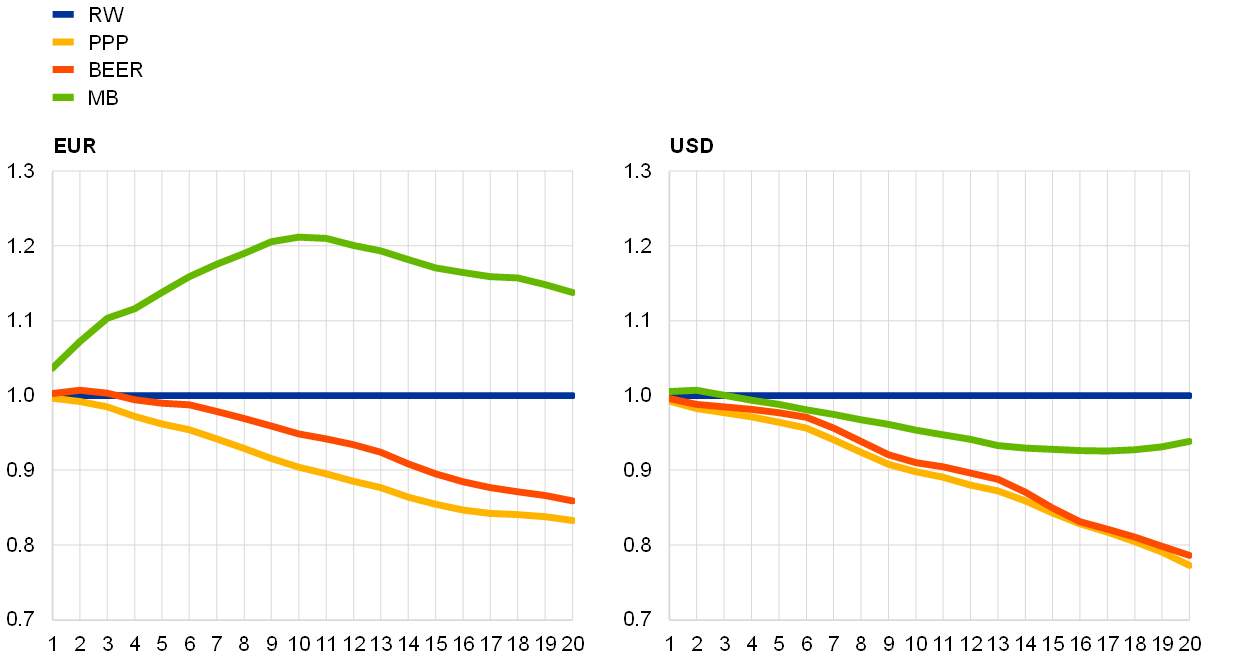
The above anecdotal evidence on the relative performance of the three models can also be shown more formally vis-à-vis the RW benchmark. To this end, in Chart 3 we plot an indicator of the performance of each model (i.e. the root mean squared forecast error – RMSFE) measured relative to the performance of the RW model. If this indicator is below unity, the model concerned delivers more accurate forecasts than those obtained using the simple assumption of an unchanged exchange rate.
Chart 3
RMSFE of the euro and the US dollar at different horizons across different models relative to the RW benchmark
a) RMSFE for real exchange rates
(index)

b) RMSFE for nominal exchange rates
(index)
Source: Authors’ calculations.
Notes: The chart shows on the y-axis the ratios of the root mean squared forecast error from the models in comparison with the RW benchmark. The x-axis is ordered in terms of quarterly horizons.
The findings confirm that the PPP and BEER models perform well in relative terms while the MB model performs poorly for the euro area. In the cases of the euro and the US dollar, the PPP model (yellow line) and the BEER model (red line) clearly outperform the RW model (blue line) in terms of forecasting both real (Chart 3, panel a) and nominal (Chart 3, panel b) exchange rates, as this indicator of forecasting performance is always below the threshold of 1. Interestingly, for the PPP model the result is already statistically significant at the one-year horizon. The MB model (green line) conversely fails to outperform the RW model in the case of the euro, while it outperforms the RW model for the US dollar at horizons longer than one year.
More mixed results are obtained for other G10 currencies. Table 2 presents the results for all countries that issue G10 currencies, with nominal and real exchange rates at the four-quarter and 20-quarter horizons. The results at short horizons show that equilibrium-based model forecasts beat the RW model forecasts approximately half of the time, albeit in only in a few instances in a significant way. However, at the longer, 20-quarter horizon, the PPP and BEER models show a stronger forecast performance than the RW model, while the MB model is generally inaccurate.[33] The PPP model is the best performing among the three models participating in the forecasting competition.
Table 2
RMSFE for real and nominal exchange rates across different models relative to the RW benchmark; estimated adjustment path

Source: Authors’ calculations.
Notes: The table shows the ratios of the root mean squared forecast error from the models in comparison with the RW benchmark, where values below unity indicate that forecasts from the respective model are more accurate than those from the benchmark. Asterisks ∗∗∗ , ∗∗ and ∗ denote respectively the 1%, 5% and 10% significance levels of the Clark-West test, where the long-run variance is calculated with the Newey-West method.
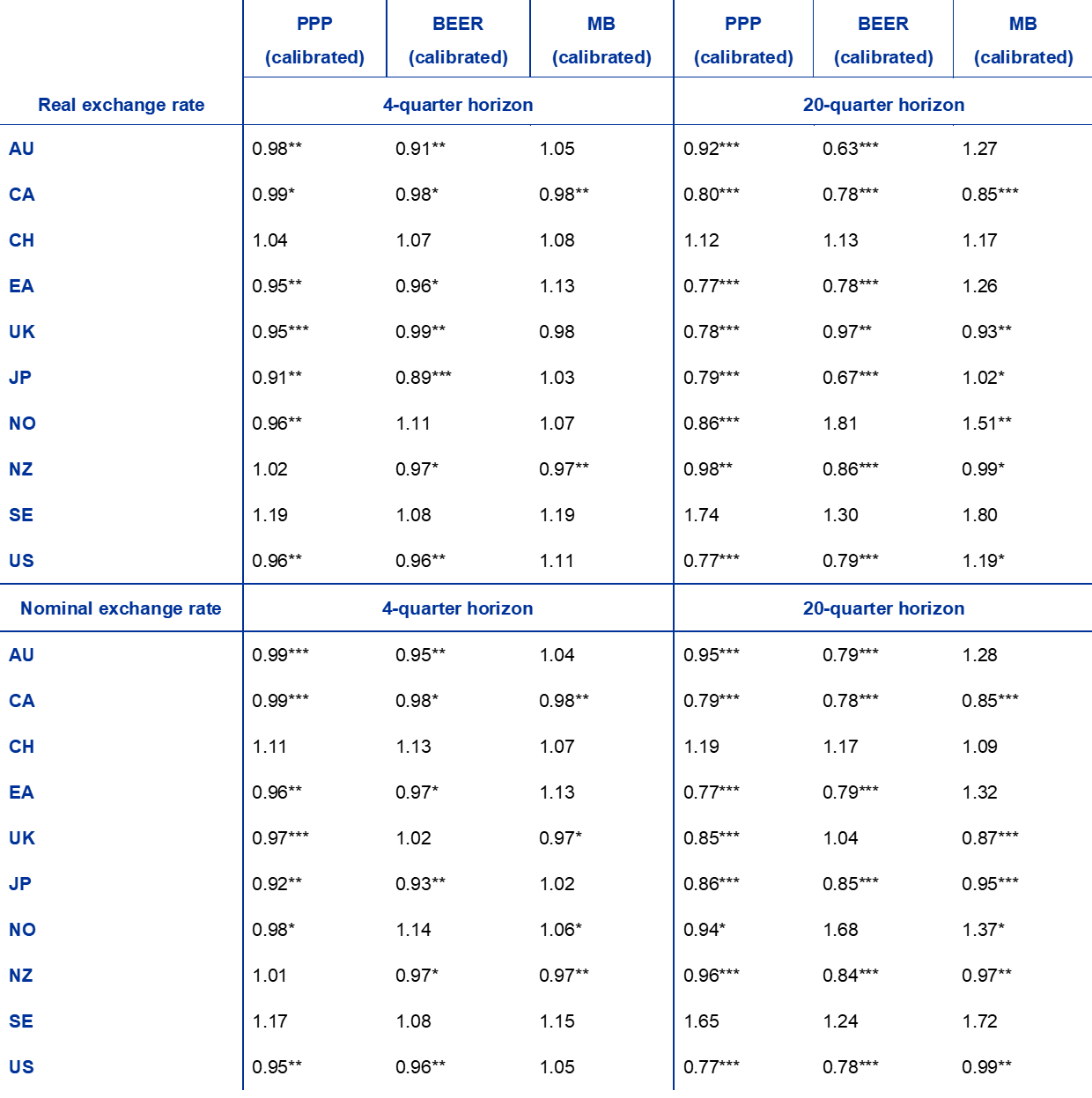
The analysis highlights that the RW model still remains a strong contender, which is most likely due to the role of estimation error. Indeed, the effort made to estimate the pace of the adjustment to equilibrium with the local projection regressions (5) and (6) has not been very helpful in terms of forecasting. To show this, the previous exercise can be repeated with the only differences being that (i) this time the nominal exchange rate moves to ensure a movement of the real exchange rate toward its equilibrium value and that (ii) such adjustment is calibrated to be rather slow in line with the real exchange rate literature. Table 3 reports the results for a half-life adjustment of three years, but the results are valid for the wider range of between two and a half years and five years, while for half-lives longer than five years the forecasts are almost the same as those given by the RW model.
Table 3
RMSFE for real and nominal exchange rates across different models relative to the RW benchmark; adjustment calibrated with a half-life of three years
Source: Authors’ calculations.
Notes: The table shows the ratios of the root mean squared forecast error from the models in comparison with the RW benchmark, where values below unity indicate that forecasts from the respective model are more accurate than those from the benchmark. Asterisks ∗∗∗ , ∗∗ and ∗ denote respectively the 1%, 5% and 10% significance levels of the Clark-West test, where the long-run variance is calculated with the Newey-West method.
The forecasting power of the PPP equilibrium exchange rate (i.e. the sample mean) becomes fully evident in this setting. The PPP model beats the RW benchmark seven times out of ten in real exchange rate forecasting and eight times out of ten in nominal exchange rate forecasting. The performance of the BEER model is almost as good as that of the PPP model, but not better as it is also affected by other sources of estimation error. The predictive power of the MB model is generally considerably worse than that of the other two models.
An additional insight gained from this result is that most of the forecasting power that the models possess relative to the RW benchmark arises directly from the mean-reverting properties of the real exchange rate.[34] It is enough to set up a simple “rule of thumb”, whereby the nominal exchange rate gradually moves to restore the real exchange rate to its mean, in order to outperform the RW model and most other models. In summary, PPP is both a competitive model in terms of equilibrium exchange rate estimation and an accurate benchmark for real and nominal exchange rate forecasting. The BEER model has good in-sample properties and a similar out-of-sample performance. Conversely, the MB model is highly unreliable in predicting future exchange rate changes.
5 Concluding remarks
Exchange rates are not a policy target for major central banks but are an important variable in their information set. They are important because anticipating their future movements could help to gauge the transmission mechanism of monetary policy. And they are important because sharp, large deviations from fair values could presage a large adjustment with potentially adverse repercussions for the outlook for inflation and for output. This article has presented an analysis bringing together the literature on equilibrium exchange rates and exchange rate forecasting. Several important, unexpected lessons can be drawn from an analysis of the predictive power of equilibrium exchange rate models.
The first is that in-sample, on average, real exchange rates tend to slowly converge to their equilibria if the latter are defined by the PPP or BEER models. This is not the case for equilibrium exchange rate models based on the current account. The equilibrium exchange rate estimates based on such models tend to be unstable and unreliable in explaining real exchange rate movements.
The second is that this convergence property can be exploited to forecast not only real exchange rates but also nominal exchange rates. The reason is intuitive as most of the adjustment toward equilibrium is achieved by a currency movement and not through relative price changes across countries. While the RW model remains, in some cases, a formidable competitor, the PPP and BEER models can help to forecast future exchange rate movements. The MB model estimates conversely are not indicative of future exchange rate movements.
The third is that most of the forecasting power comes from the mean-reverting properties of real exchange rates rather than from exploiting the relationship between exchange rates and economic fundamentals. While the notion of PPP is much more compatible with economic theory and hence offers reassurance as to the usefulness of macroeconomic theory and the role of the exchange rate in the transmission of monetary policy, the original insight of Meese and Rogoff (1983) – that the future path of exchange rates cannot easily be better extrapolated from economic models than by using a “rule of thumb” – remains largely true. In this article we have qualified this result by suggesting that the most competitive “rule of thumb” is often one which foresees a gradual adjustment of the exchange rate to restore the real exchange rate to its mean value rather than one that assumes “no change”. The key fundamentals that need to be known for out-of-sample forecasting are the real and nominal exchange rates, while there is relatively little information to be extracted from other economic fundamentals in normal times. Large current account surpluses or deficits may influence the path of adjustment of the exchange rate but, in line with theory, they have a limited influence on the long-term value of the exchange rate.
- This article has benefited from helpful comments by Philip Lane, Fabio Panetta, Livio Stracca, João Sousa, Michael Fidora, David Lodge, Arnaud Mehl, Chiara Osbat and Alexandra Buist.
- Meese, R. A. and Rogoff, K., “Empirical exchange rate models of the seventies: Do they fit out of sample?”, Journal of International Economics, Vol. 14(1-2), 1983, pp. 3-24. The authors showed that these results hold even when the models have the advantage of using known, realised economic fundamentals. A theoretical explanation of these findings is presented by Engel et al. (2008), who showed that, under certain conditions, model-based forecasts may be less accurate than an RW benchmark, even if the model reflects the true underlying data-generating process. For more details, see Engel, C., Mark, N.C. and West, K.D., “Exchange rate models are not as bad as you think”, in Acemoglu, D., Rogoff, K. and Woodford, M. (eds.), NBER Macroeconomics Annual 2007, Vol. 22 of NBER Chapters, National Bureau of Economic Research, 2008, pp. 381–441.
- Rogoff, K., comment on the paper by Engel, C., Mark, N.C. and West, K.D., “Exchange rate models are not as bad as you think”, in Acemoglu, D., Rogoff, K. and Woodford, M. (eds.), NBER Macroeconomics Annual 2007, Vol. 22 of NBER Chapters, National Bureau of Economic Research, 2008, pp.443–452, https://www.nber.org/system/files/chapters/c4076/c4076.pdf
- Rossi, B., “Exchange rate predictability”, Journal of Economic Literature, Vol. 51, 2013, pp. 1063-1119.
- Cheung, Y.-W., Chinn, M.D., Pascual, A.G. and Zhang, Y., “Exchange rate prediction redux: New models, new data, new currencies”, Journal of International Money and Finance, Vol. 95, 2019, pp. 332–336.
- For a review of the role of the exchange rate in the case of the ECB, see the Work Stream on Globalisation, “The implications of globalisation for the ECB monetary policy strategy”, Occasional Paper Series, No 263, ECB, September 2021.
- The concept and measurement of the equilibrium exchange rate is particularly relevant also for central banks adopting managed exchange rate regimes or for countries joining the exchange rate mechanism and later fixing their parity irrevocably to the euro.
- Bussière, M., Ca’ Zorzi, M., Chudik, A. and Dieppe, A., “Methodological advances in the assessment of equilibrium exchange rates”. Working Paper Series, No 1151, European Central Bank, 2010; Phillips, S., Catao, L., Ricci, L.A., Bems, R., Das, M., di Giovanni, J., Unsal, D.F., Castillo, M., Lee, J., Rodriguez, J. and Vargas, M., “The External Balance Assessment (EBA) Methodology”, IMF Working Papers, No 13/272, International Monetary Fund, 2013; Couharde, C., Delatte, A.L., Grekou, C., Mignon, V. and Morvillier, F., “EQCHANGE: A world database on actual and equilibrium effective exchange rates”, International Economics, Vol. 156, 2018, pp. 206–230; Cubeddu, L.M., Krogstrup, S., Adler, G., Rabanal, P., Dao, M.C., Hannan, S.A., Juvenal, L., Buitron, C.O., Rebillard, C., Garcia-Macia, D. and Jones, C., “The External Balance Assessment Methodology: 2018 Update”, IMF Working Papers, No 19/65, International Monetary Fund, 2019.
- Ca’ Zorzi, M., Muck, J. and Rubaszek, M., “Real exchange rate forecasting and PPP: This time the random walk loses”, Open Economies Review, Vol. 27, 2016, pp. 585–609; Ca’ Zorzi, M. and Rubaszek, M., “Exchange rate forecasting on a napkin”, Journal of International Money and Finance, Vol. 104, 2020.
- This property is also partly embedded in theoretical sticky price models. However, in these models the obtained co-movement between real and nominal exchange rates tends to be smaller than in the actual data.
- Ca’ Zorzi, M., Kolasa, M. and Rubaszek, M., “Exchange rate forecasting with DSGE models”, Journal of International Economics, Vol. 107, 2017, pp. 127–146.
- Eichenbaum, M., Johannsen, B.K. and Rebelo, S., “Monetary policy and the predictability of nominal exchange rates”, The Review of Economic Studies, Vol. 88, 2020, pp. 192–228.
- In particular, this Economic Bulletin article updates the results that are described in detail in the study by Ca’ Zorzi, M., Cap, A., Mijakovic, A. and Rubaszek, M., “The reliability of equilibrium exchange rate models: A forecasting perspective”, International Journal of Central Banking, forthcoming. A previous version of this paper is available as ECB Working Paper No 2358.
- Driver, R. and Westaway, P., “Concepts of equilibrium exchange rates”, Bank of England Working Paper, No 248, Bank of England, 2005.
- Examples of these models are found in Ca’ Zorzi, M., Kolasa, M. and Rubaszek, M., 2017, op. cit.; Eichenbaum, M., Johannsen, B.K. and Rebelo, S., 2020, op. cit.; and Itskhoki, O. and Mukhin, D., “Exchange rate disconnect in general equilibrium”, Journal of Political Economy, Vol. 129(8), 2021.
- This notion is implicit in the uncovered interest rate parity as discussed in Engel, C., “Exchange rates, interest rates, and the risk premium”, American Economic Review, Vol. 106, 2016, pp. 436-474.
- Cassel, G., “Abnormal deviations in international exchanges” Economic Journal, December 1918, pp. 413–415.
- Fell, J., “Balance of payments equilibrium and long-run real exchange rate behaviour”, mimeo, European Monetary Institute, 1996; MacDonald, R., “What determines real exchange rates?: The long and the short of it”, Journal of International Financial Markets, Institutions and Money, Vol. 8, 1998, pp. 117–153; Maeso-Fernandez, F., Osbat, C. and Schnatz, B., “Determinants of the Euro Real Effective Exchange Rate: A BEER/PEER Approach”, Australian Economic Papers, Vol. 41(4), 2002, pp. 437–461; Lee, J., Ostry, J.D., Prati, A., Ricci, L.A. and Milesi-Ferretti, G.M., “Exchange Rate Assessments: CGER Methodologies”, IMF Occasional Papers, No 261, International Monetary Fund, 2008.
- Fidora, M., Giordano, C. and Schmitz, M., “Real exchange rate misalignments in the euro area”, Working Paper Series, No 2108, European Central Bank, 2017.
- Lee, J., Milesi-Ferretti, G.M. and Ricci, L.A., “Real exchange rates and fundamentals: A cross-country perspective”, Journal of Money, Credit and Banking, Vol. 45, 2013, pp. 845–865; and Zhang, Q., “The Balassa-Samuelson relationship: Services, manufacturing and product quality”, Journal of International Economics, Vol. 106, 2017, pp. 55–82.
- Lane, P.R. and Milesi-Ferretti, G.M., “External wealth, the trade balance, and the real exchange rate”, European Economic Review, Vol. 46, 2002, pp. 1049–1071.
- Faruqee, H., “Long-run determinants of the real exchange rate: a stock-flow perspective”, IMF Staff Papers, Vol. 42, 1995, pp. 80–107; Lane, P.R. and Milesi-Ferretti, G.M., “The transfer problem revisited: Net foreign assets and real exchange rates”, The Review of Economics and Statistics, Vol. 86, 2004, pp. 841–857. As explained in Lane and Milesi-Ferretti, this specification represents a long-run cointegration relationship, necessitating panel cointegration estimators.
- See Williamson, J., (ed.) Estimating Equilibrium Exchange Rates, Institute for International Economics, 1994; and Lee et al. (2008), op. cit.
- This consists in forecasting the underlying current account with an RW model, defining the current account norm based on a panel regression and choosing appropriate current account elasticities.
- For evidence of the large amount of uncertainty surrounding the estimation of trade elasticities, see Bussière at al. (2010), op. cit. For the baseline we have assumed producer currency pricing. This means that export prices do not react to exchange rate changes, whereas import prices are affected one-to-one, implying perfect pass-through. Given the large estimation uncertainty regarding the magnitude of foreign trade elasticities, we followed the literature and set the long-run price elasticities equal to minus one. These assumptions translate into a set of elasticities that are both country- and time-dependent as they are a function of import and export shares. For evidence of the impact on the forecasting performance of the three models using different currency pricing assumptions, see Ca’ Zorzi et al. (2022), op. cit.
- Opie, W. and Riddiough, S.J., “Global currency hedging with common risk factors”, Journal of Financial Economics, Vol. 136, 2020, pp. 780–805; and Engel, C. and Wu, S.P.Y. (2021), op. cit.
- For each of the ten analysed economies, the foreign sector is represented by the other nine countries plus Denmark, which is excluded from the analysis owing to its fixed exchange rate regime. The weights are computed based on the narrow effective exchange rate index published by the Bank for International Settlements (BIS). We take BIS weights for the year 1995 and adjust them so that they sum to unity. The exact values are presented in Table 1 in Ca’ Zorzi et al. (2022), op. cit., and cover 75% to 96% of the BIS index.
- The panel results are estimated using fixed effects for the ten countries in the sample and correcting errors for autocorrelation and heteroskedasticity.
- For the PPP model the ratio of nominal to real adjustment, tends to be below unity, which means that a small fraction of the real exchange rate adjustment is completed by relative inflation.
- At the four-year horizon there is evidence of overshooting in the case of the euro and the US dollar, suggesting that the estimated misalignment flips in the opposite direction.
- A similar result is found by Yesin (2016). See Yesin, P., “Exchange rate predictability and state-of-the art models”, SNB Working Paper Series, No 2/2016, Swiss National Bank, 2016.
- This can be explained by two factors: high volatility of the MB-implied equilibria and low estimates of the adjustment parameter , which suggests that there is limited convergence to equilibrium for current account-based equilibrium exchange rate models. If is close to nil, forecasts calculated with equation (4) resemble those that would be obtained using an RW model with a drift, which is the case for the MB model. This confirms our in-sample insight of a very limited adjustment of exchange rates toward equilibrium exchange rate estimates when the latter are derived with the MB model.
- A similar result is found in Yesin (2016), op. cit. The analysis shows that, despite the usefulness of the MB model in the context of the global imbalances debate, the BEER model has stronger forecasting properties.
- A similar conclusion is reached by Engel and Wu (2021), op. cit., by showing that the mean-reverting property of the bilateral US dollar exchange rate can be exploited in nominal exchange rate forecasting, while additional explanatory variables, like the risk premium, do not improve the predictability of the nominal exchange rate out-of-sample.


